My last experiments have analysed different conformations of ethane and butane where I've used MolecCuilder to calculate the ground-state energy of various configurations of these two molecules. FOr example, butane I've rotated around its central bond in equidistant steps. This allowed me to compare the resulting potential barriers against the literature.

I'm still on this train of thought: Directly connected to these potential barriers is the question of stability. Given a molecule and a specific configuration, how can I assess the (thermal) stability from ab-initio calculations? And the other question I had in mind: How can I extend this analysis to other (small, organic) molecules?

I will look at the second question first: My inspiration was an article by a former colleague of mine ​[Israels, Maaß, Hamaekers, 2017] on the octet rule in chemical space, Basically, they are generating -- what I call -- saturated molecules using the octet rule (i.e. fully occupied electron orbitals).

It was a low-hanging fruit to add this as some of the necessary ingredients have already been present in MoleCuilder.

1. Saturation of non-hydrogen atoms by placing hydrogens along pre-computed vertices of polyhedra (e.g., for carbon with the four important sp-orbitals, we look at the four corners of a tetrahedra).
2. Encoding knowledge of occupied and unoccupied orbitals per element (e.g., the specific angle in water is mostly because two corners of a tetrahedra are picked)

I then created a larger python script using the pyMoleCuilder library that does the following steps:

1. Start with a "seed" atom in the center of the domain.
2. Saturate the atom.
3. Pick randomly a number of newly added hydrogens (up to a maximum, e.g., 3).
4. Replace this set of picked hydrogens by a single new non-hydrogen atom of a chosen element using the mean position of the hydrogens.
5. Rescale the bond between old and new non-hydrogen atom to typical tabularized bond length (in MoleCuilder called "bond table").
6. Step to the new non-hydrogen.
7. When enough non-hydrogen atoms have been added, stop. Otherwise, go to step 2.
8. Calculate ground-state energy or optimize the created configuration.

In order to then generate "all" molecules of a given set of elements (I've picked {C,N,O}), I don't use random picking but the powerset of all hydrogens up till a given number and execute the procedure for every powerset combination.

One small challenge is the naming. I wanted a representation of the bond graph in the name. Informatics knows all about graphs and there's also a format for specifying them: graph6. There's even tools and websites to generate all (connected) graphs up to certain vertex count: See the ​[House of Graphs] and ​[nauty], on searching and generating graphs. I've added a small action to MoleCuilder that gives the currently selected molecule in graph6 representation and that uses BFS to give the element list starting from the least-connected non-hydrogen atom (ignoring hydrogens).

Let me show you the result for N=1.

graph6	elements	chemical formula	molecule name	energy [Ht]	largest force [Ht]	num neg EV	configuration
Ds_	C	CH4	​Methane	-40.181	5.06882e-10 2.80043e-10 6.06817e-10	18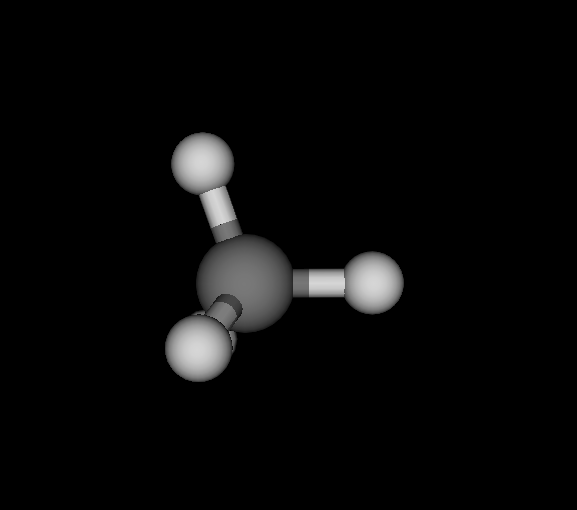
Cs	N	NH3	​Ammonia	-56.166	2.02605e-05 2.88662e-05 4.92678e-05	16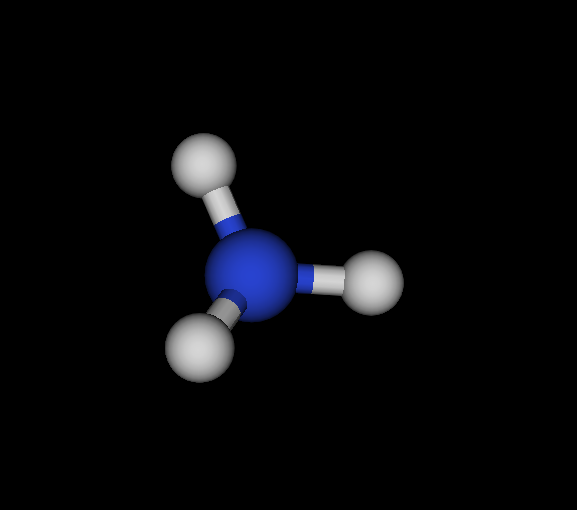
Bo	O	OH2	​Water	-75.985	8.22233e-09 1.18472e-08 2.90999e-11	14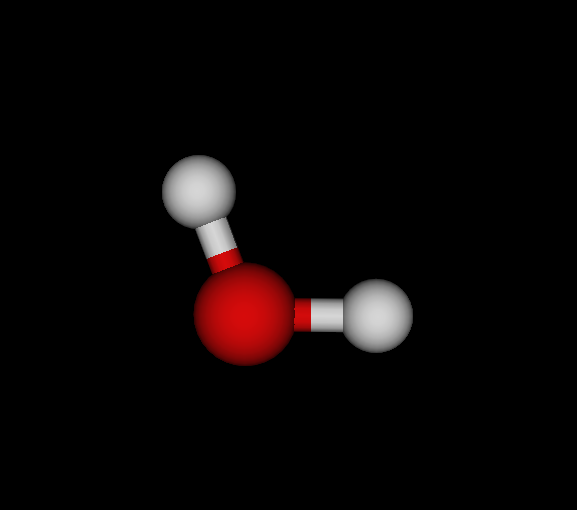

You find the graph6 string (of full graph including hydrogens) first, then the list of elements, the chemical formula and the molecule's name. Moreover, I give the ground state energy (see below for details), the largest remaining force component per dimension and number of negative eigenvectors. Finally, a small graphical representation of the optimized structure (automated snapshot taken with molecuildergui using a small python script). The most important bit about this: It's completely automated. I'm just giving the parameters, run the whole experiment and the output is the above table.

Energy calculations have been done in 6-31G basis (mostly for reasons of computational ease, not accuracy) and either Closed-Shell Hartree-Fock (CLHF) or Moeller-Plesset Perturbation Theory second order (MBPT). As you see, O and C are well-optimized, N is not yet. However, my goal here is not to give accurate ground-state configurations and energies but just show what's possible.

The tables for N from 1 up till 3 are given in the attachments, where you also find the necessary script files.

It's been quite a while since analysis_ethane, where I suggested that a look at butane might be interesting, too, as its structure of conformers is richer. As you can see by the following screenshots from MoleCuilder, there are four conformers.

syn/eclipsed methyl	gauche	120/eclipsed	anti

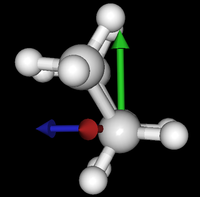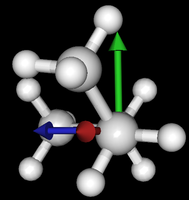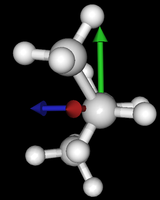However, the more complex an experiment, the more prone one is to making errors as well. I have made quite many: overwritten output files, stumbling over the limited precision of PDB files (use tremolo format if you're optimizing to very high precision), confusion when using the Python interface because of no "named arguments" support so far (contained in upcoming v1.6.1), copy&paste errors when building on the script I used for ethane.

But one thing especially impeded me: The quality of the optimization.

If one plans on investigating butane's rotational barriers, then one should have a fully annealed "anti" conformer state at hand.

But to make a long story short, here it is:

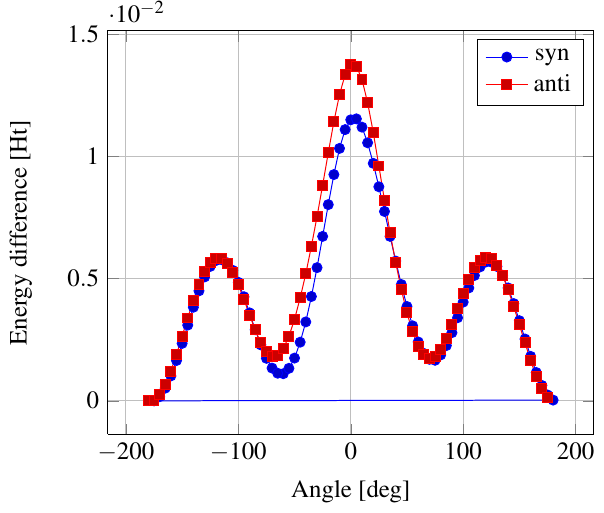
As you see in the conformer screenshots, I have done the rotation around the middle CC bond in the same manner as with ethane before. The conformer names relate to the following angles: syn (0°), gauche (60°), 120 (120°), anti (180°). I used two initial states: an optimized "syn" and an optimized "anti" state - both optimized to 1e-5 a.u. absolute error in energy in roughly 2000 steps. I have used 6-31G basis set and CLHF theory for optimization and rotation. If you'd like to reproduce the figure, using the docker image, both optimized conformer states are attached to this blog post including the update script to rotate around the CC bond and compute the energy. You need MoleCuilder version 1.6.1 which is soon to be released.

You notice that the two minima left and right of the central peak are not the same when starting from the "syn" state. They both correspond to the symmetric state of the same conformer. This is a clear indication that one needs to start from the lowest energy state, which is "anti". On the other hand, there is an energy difference in the central peak when starting from either state.

Comparing the above with experimental data at ​introorganicchemistry, you'll notice that the central peak is strongly overestimated by theory. However, a recent article by ​[Yirong Mo, JOCNote, 2012] states that experimental data and theoretical predictions do not match. This is why there are articles such as ​[Murcko, Castejon, Wiberg, 1996] and ​[Allinger, Fermann, Allen, Schaefer, JCP, 1997] calculating the energy differences to very high precision, estimating the syn/anti difference at around 0.087 Ht, while experimentally it is just 0.006 Ht, in chemical units 3.78 kcal/mole.

Here, we notice that the "syn" state is closer to the true energy difference as expected from theory, namely 0.0115 Ht. Note that ​[Yirong Mo, JOCNote, 2012] obtains roughly 0.01 Ht using Moeller-Plesset 2nd order and 6-31G(d) (with diffuse basis functions) where he optimized in each rotational step.

Having not optimized each step itself, I am satisfied with the results.

In today's blog entry we look at the simple ethane molecule. More precisely, we interested in the rotational change between two of its conformations: staggered and the eclipsed.

We are interested in the energy barrier between these two conformations.

Let's first build the ethane molecule from scratch. We fire up molecuildergui and add two carbon atoms about 1.6 Angström apart from one another using add-atom. Then, we add hydrogens with saturate-atoms after having selected both carbons (either by clicking on them) or using select-all-atoms. The result looks quite reasonable already but the structure is not optimized. This we make up leeway by optimize-structure with 500 steps at a deltat of 2.5, all force components are then below 7e-7 a.u.. Note that beforehand we have used set-parser-parameters of mpqc to have a basis set of 6-31G and theory to MBPT2, moreover used random-perturbation with set-random-number-distribution as uniform_01 to randomly perturb all positions by at most 0.05 Angström. The latter shakes the configuration out of any possible unstable equilibrium. We obtain a final energy of -79.38819 Ht.

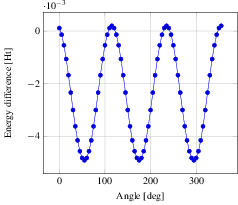
Now we step on to the actual analysis of the conformational change. We use a little python script (see C2H6_rotate-bond.py​) using the python module pyMolecuilder of MoleCuilder (version 1.6.1). The script rotates via rotate-around-bond one end of the ethane molecule by a prescribed angle, where we use select-atom-by-element to select both carbon atoms and thus specifying the bond around which to rotate. In total we go through the 360 degrees in steps of 5 degrees. After each rotation, the energy of the molecule in vacuum is calculated using MPQC by the action triplet fragment-molecule, fragment-automation, analyse-fragment-results. Before each rotation, we step on to the next discrete time step using step-world-time such that we obtain the complete trajectory of the rotation on output via output-as.

In the figure we see nicely the change in energy between the staggered and the eclipsed conformation, each occurring thrice over the range of 360 degrees. Note that we plot against the lowest energy of -79.38819027 Ht, hence negative difference actually means a higher energy. From the graph we read off the energy difference as roughly 0.005 Ht, equivalent to 0.136 eV. At room temperature of 300 Kelvin, we have a average thermal energy of 0.026 eV. Hence, the eclipsed state's probability is about $\exp(-0.136eV/(k_B * 300 K)) = 0.0052$ with respect to the staggered one, i.e. ethane will remain mostly in the staggered state.

For a nicer and more elaborate discussion of the underlying chemistry, see ​here. There, it is suggested to look also at butane. And one should replace one hydrogen atom on either end of the ethane molecule by a methyl group.

But we will leave this for the next blog entry ...