Walking the Chemical Space

My last experiments have analysed different conformations of ethane and butane where I've used MolecCuilder to calculate the ground-state energy of various configurations of these two molecules. FOr example, butane I've rotated around its central bond in equidistant steps. This allowed me to compare the resulting potential barriers against the literature.

I'm still on this train of thought: Directly connected to these potential barriers is the question of stability. Given a molecule and a specific configuration, how can I assess the (thermal) stability from ab-initio calculations? And the other question I had in mind: How can I extend this analysis to other (small, organic) molecules?

I will look at the second question first: My inspiration was an article by a former colleague of mine ​[Israels, Maaß, Hamaekers, 2017] on the octet rule in chemical space, Basically, they are generating -- what I call -- saturated molecules using the octet rule (i.e. fully occupied electron orbitals).

It was a low-hanging fruit to add this as some of the necessary ingredients have already been present in MoleCuilder.

1. Saturation of non-hydrogen atoms by placing hydrogens along pre-computed vertices of polyhedra (e.g., for carbon with the four important sp-orbitals, we look at the four corners of a tetrahedra).
2. Encoding knowledge of occupied and unoccupied orbitals per element (e.g., the specific angle in water is mostly because two corners of a tetrahedra are picked)

I then created a larger python script using the pyMoleCuilder library that does the following steps:

1. Start with a "seed" atom in the center of the domain.
2. Saturate the atom.
3. Pick randomly a number of newly added hydrogens (up to a maximum, e.g., 3).
4. Replace this set of picked hydrogens by a single new non-hydrogen atom of a chosen element using the mean position of the hydrogens.
5. Rescale the bond between old and new non-hydrogen atom to typical tabularized bond length (in MoleCuilder called "bond table").
6. Step to the new non-hydrogen.
7. When enough non-hydrogen atoms have been added, stop. Otherwise, go to step 2.
8. Calculate ground-state energy or optimize the created configuration.

In order to then generate "all" molecules of a given set of elements (I've picked {C,N,O}), I don't use random picking but the powerset of all hydrogens up till a given number and execute the procedure for every powerset combination.

One small challenge is the naming. I wanted a representation of the bond graph in the name. Informatics knows all about graphs and there's also a format for specifying them: graph6. There's even tools and websites to generate all (connected) graphs up to certain vertex count: See the ​[House of Graphs] and ​[nauty], on searching and generating graphs. I've added a small action to MoleCuilder that gives the currently selected molecule in graph6 representation and that uses BFS to give the element list starting from the least-connected non-hydrogen atom (ignoring hydrogens).

Let me show you the result for N=1.

graph6	elements	chemical formula	molecule name	energy [Ht]	largest force [Ht]	num neg EV	configuration
Ds_	C	CH4	​Methane	-40.181	5.06882e-10 2.80043e-10 6.06817e-10	18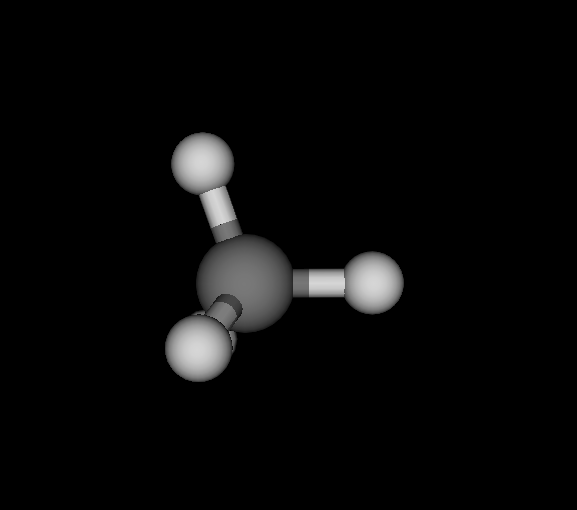
Cs	N	NH3	​Ammonia	-56.166	2.02605e-05 2.88662e-05 4.92678e-05	16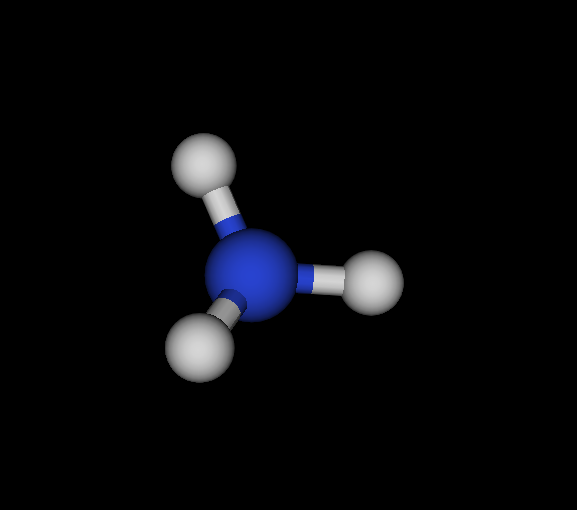
Bo	O	OH2	​Water	-75.985	8.22233e-09 1.18472e-08 2.90999e-11	14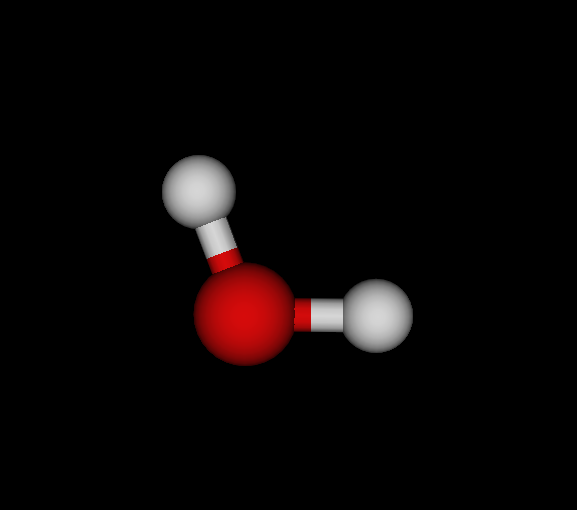

You find the graph6 string (of full graph including hydrogens) first, then the list of elements, the chemical formula and the molecule's name. Moreover, I give the ground state energy (see below for details), the largest remaining force component per dimension and number of negative eigenvectors. Finally, a small graphical representation of the optimized structure (automated snapshot taken with molecuildergui using a small python script). The most important bit about this: It's completely automated. I'm just giving the parameters, run the whole experiment and the output is the above table.

Energy calculations have been done in 6-31G basis (mostly for reasons of computational ease, not accuracy) and either Closed-Shell Hartree-Fock (CLHF) or Moeller-Plesset Perturbation Theory second order (MBPT). As you see, O and C are well-optimized, N is not yet. However, my goal here is not to give accurate ground-state configurations and energies but just show what's possible.

The tables for N from 1 up till 3 are given in the attachments, where you also find the necessary script files.